This post is part two of a series about how to extend cloud-based data analysis tools – such as Google’s BigQuery ML – to handle specific econometrics requirements. In part 1, I showed how to compute coefficient standard errors in BigQuery. Often, however, heteroskedasticity or autocorrelation in the data means that the regression variance estimates – and thus the standard errors – will be biased.
The solution to the heteroskedasticity standard error problem is to estimate robust standard errors (also known as Huber-White standard errors). These can be calculated easily in Stata using the robust option following most regression commands, or in R using the sandwich package and the vcovHC command. But what about in BigQuery?
The formula for Huber-White robust standard errors is
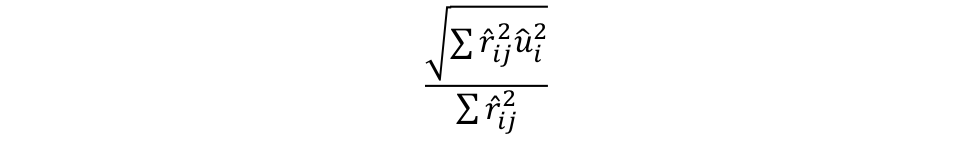
Where ûi is the residual from the original regression and r̂ij is the residual from the regression of regressor j on the rest of the regressors. Optionally, we can perform a degrees of freedom correction by multiplying this formula by n/(n-k-1), but as n is large and k is relatively small, the correction is close enough to 1 that we can ignore it.
While this formula is slightly more complicated to implement than the one for regular standard errors (as terms have not already been computed by BigQuery), it can still be computed relatively easily. First, for each variable we compute the regression of the remaining variables onto that one as we did for the ordinary standard errors. We then compute the residuals using the predicted value, and with simple arithmetic compute the standard errors.
To compute the residuals, we can either use BigQuery’s ML.PREDICT to predict the values of the dependent variable or calculate the values directly from the coeffients. Because we’re combining many regressions, it’s slightly easier to calculate them without ML.PREDICT. First, get the coefficients:
SELECT processed_input, weight
FROM ML.WEIGHTS(MODEL `<dataset>.<model_name >`)This query yields the weight (coefficient) for each input and the intercept term, from which we can create an equation to predict a term. That is, we take the coefficients (weights) and multiply them by the variable name, plus the intercept term.
UPDATE `<dataset>.<data>`
SET residual_<term> = predicted_<term> - <term>
WHERE residual_<term> is nullWe can then calculate the numerator in the Huber-White robust standard error equation:
SELECT SQRT(SUM(POW(residual_<term>, 2) * POW(residual_<regressand>, 2)))
FROM `<dataset>.<data>`and the denominator:
SELECT SUM(POW(residual_<term>, 2))
FROM `<dataset>.<data>`The next step is to divide the numerator and denominator (or combine the two previous equations into one query to divide them), giving us the robust standard error.
As in part one, we can use Python to reduce the repetitiveness of the queries, like so:
#Nathaniel Lovin
#Technology Policy Institute
#
#!/usr/bin/env python
from google.cloud import bigquery
import math
import sys
from scipy.stats import t
client = bigquery.Client()
def addColumns(dataset, data, coeffs, regressand):
table_ref = client.dataset(dataset).table(data)
table = client.get_table(table_ref)
original_schema = table.schema
new_schema = original_schema[:]
for coeff in coeffs.keys():
if coeff != "__INTERCEPT__":
new_schema.append(bigquery.SchemaField("predicted_" + coeff, "FLOAT"))
new_schema.append(bigquery.SchemaField("residual_" + coeff, "FLOAT"))
new_schema.append(bigquery.SchemaField("predicted_" + regressand, "FLOAT"))
new_schema.append(bigquery.SchemaField("residual_" + regressand, "FLOAT"))
table.schema = new_schema
table = client.update_table(table, ["schema"])
assert len(table.schema) == len(original_schema) + 2*len(coeffs.keys()) == len(new_schema)
def predict(dataset, data, prediction, coefficients):
regression = ""
for coeff in coefficients.keys():
if coeff != "__INTERCEPT__":
regression += str(coefficients[coeff]['coefficient']) + "*" + coeff + " + "
else:
regression += str(coefficients[coeff]['coefficient']) + " + "
regression = regression[:-3]
query = ("UPDATE `" + dataset + "." + data + "` SET predicted_" + prediction + " = " + regression + " WHERE predicted_" + prediction + " is null")
query_job = client.query(query)
result = query_job.result()
def residuals(dataset, data, variable):
query = ("UPDATE `" + dataset + "." + data + "` SET residual_" + variable + " = predicted_" + variable + " - " + variable + " WHERE residual_" + variable + " is null")
query_job = client.query(query)
result = query_job.result()
def squareSum(dataset, data, variable):
query = ("SELECT SUM(POW(residual_" + variable + ", 2)) FROM `" + dataset + "." + data + "`")
query_job = client.query(query)
result = query_job.result()
for row in result:
return row.f0_
def topSum(dataset, data, variable, regressand):
query = ("SELECT SUM(POW(residual_" + variable + ", 2) * POW(residual_" + regressand + ", 2)) FROM `" + dataset + "." + data + "`")
query_job = client.query(query)
result = query_job.result()
for row in result:
return row.f0_
def coefficients(dataset, model_name):
coeffs = {}
query = ("SELECT processed_input, weight FROM ML.WEIGHTS(MODEL `" + dataset + "." + model_name + "`)")
query_job = client.query(query)
result = query_job.result()
for row in result:
coeffs[row.processed_input] = {}
coeffs[row.processed_input]['coefficient'] = row.weight
return coeffs
def regressions(dataset, data, coeffs, regressand):
for coeff in coeffs.keys():
query = ("CREATE OR REPLACE MODEL `" + dataset + "." + coeff + "` "
"OPTIONS (model_type='linear_reg', input_label_cols=['" + coeff + "']) AS "
"SELECT " + ", ".join(coeffs.keys()) + " FROM `" + dataset + "." + data + "` WHERE " + " is not NULL and ".join(coeffs.keys()) + " is not NULL")
query_job = client.query(query)
result = query_job.result()
model_coeffs = coefficients(dataset, coeff)
predict(dataset, data, coeff, model_coeffs)
residuals(dataset, data, coeff)
coeffs[coeff]["top"] = math.sqrt(topSum(dataset, data, coeff, regressand))
coeffs[coeff]["bottom"] = squareSum(dataset, data, coeff)
error = coeffs[coeff]["top"]/coeffs[coeff]["bottom"]
coeffs[coeff]["standard error"] = error
return coeffs
dataset = sys.argv[1]
data = sys.argv[2]
model_name = sys.argv[3]
regressand = sys.argv[4]
n = int(sys.argv[5])
coeffs = {}
coeffs = coefficients(dataset, model_name)
addColumns(dataset, data, coeffs, regressand)
predict(dataset, data, regressand, coeffs)
residuals(dataset, data, regressand)
coeffs.pop("__INTERCEPT__")
coeffs = regressions(dataset, data, coeffs, regressand)
for coeff in coeffs.keys():
coeffs[coeff]['tstat'] = coeffs[coeff]['coefficient']/coeffs[coeff]['standard error']
coeffs[coeff]['pvalue'] = 2*t.sf(abs(coeffs[coeff]['tstat']), n-len(coeffs.keys())-1)
for coeff in coeffs.keys():
print(coeff + " coefficient: " + str(coeffs[coeff]['coefficient']))
print(coeff + " standard error: " + str(coeffs[coeff]['standard error']))
print(coeff + " t-stat: " + str(coeffs[coeff]['tstat']))
print(coeff + " p-value: " + str(coeffs[coeff]['pvalue']))And running it as python BigQueryRobustSE.py <dataset> <data> <model_name> <regressand> <n>, where <dataset> is the BigQuery dataset where your model and data are located, <data> is the BigQuery table with your data, <model_name> is the name of the original BigQuery ml model, <regressand> is the dependent variable of the original regression, and <n> is the size of the sample.
To show how these work, let’s compare the output of this program to the output of Stata and R for the same regressions. We’ll use the “CollegeDistance” dataset from applied economics in R (https://cran.r-project.org/web/packages/AER/AER.pdf).The “CollegeDistance” dataset has 4739 observations so the degrees of freedom correction is smaller and the comparison should be close.
| Unemployment | Distance | Tuition | ||
| Stata | Coefficient | .1110363 | -.023334 | 1.07464 |
| Standard Error | .0070001 | .0083202 | .0547596 | |
| Robust Standard Error | .006841 | .0082369 | .0388905 | |
| R | Coefficient | 0.111036 | -0.02333 | 1.07464 |
| Standard Error | 0.00700 | 0.00832 | 0.05476 | |
| Robust Standard Error | 0.006838 | 0.008233 | 0.038874 | |
| BigQuery | Coefficient | 0.1110363 | -0.02333 | 1.07464 |
| Standard Error | 0.0069 | 0.00815 | 0.05416 | |
| Robust Standard Error | 0.006833 | 0.008222 | 0.03896 |
Now we have Huber-White Standard Errors in BigQuery. Eventually, I will show the other robust standard error, Newey-West, but in the next post I will show how to perform Two Stage Least Squares in BigQuery.


