Traditionally, econometric and statistical data analysis have been, and continue to be, done on local PCs. The tools of choice typically include STATA, R, SPSS, and some others, and have been for decades. Meanwhile, data storage and computer processing at levels unheard of even a few years ago has become available in the cloud to everyone.
While econometric and statistical packages like STATA for local computation have evolved extensively, such tools on the cloud are new and not nearly as extensive. In order to speed our own big data analyses, we have had to expand the set of tools available in the cloud. This blog post elaborates on our efforts and makes the results available to others to use and, hopefully, improve.
Specifically, we’ve been attempting to use BigQuery ML’s linear regression feature to do certain regressions more quickly than we could do locally on STATA. Out of the box, however, BigQuery ML is missing some important econometric features. In this series of posts, I will be showing how to extend the BigQuery ML results with some simple SQL code.
Calculating Standard Errors
A key part of any regression is understanding the statistical significance of the estimated coefficients, yet BigQuery ML’s linear regression feature does not calculate standard errors. In this first post, I show how to calculate the standard errors of the coefficients.
The sample coefficient standard errors is calculated as
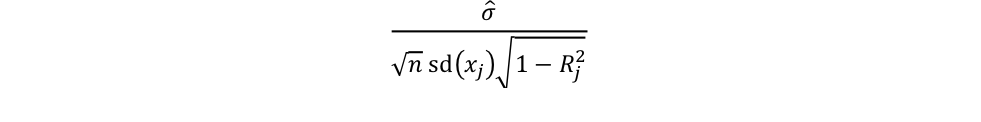
where ?̂ is the standard error of the regression, n is the size of the sample, sd(xj) is the standard deviation of regressor j, and Rj2 is the correlation between regressor j and the rest of the regressors.
The standard error of the regression is also called the root mean squared error. The mean squared error can be found using Big Query ML’s ML.EVALUATE function, and the root mean squared error is simply its square root. That is:
SELECT
sqrt(mean_squared_error) as root_mean_squared_error
FROM
ml.EVALUATE(MODEL <model name>, (SELECT * FROM <dataset>))n, the sample size, is specified when you construct the model and thus is already known.
The standard deviation of each regressor is found in ML.FEATURE:
SELECT input, stddev FROM
ML.FEATURE_INFO(MODEL <model>)What Big Query ML does not readily provide is the correlation between the regressors. To calculate these cross-correlations, we regress the rest of the independent variables onto each one, and obtain the r-squared:
CREATE OR REPLACE MODEL `dataset.var1`
OPTIONS (model_type='linear_reg', input_label_cols=['var1']) AS
SELECT
var1,
var2,
Var3
FROM
<dataset>
WHERE
var1 is not NULL and var2 is not NULL and var3 is not NULLSELECT
r2_score
FROM
ml.EVALUATE(MODEL `dataset.var1`)Of course, repeating these commands for many variables would be tedious and impractical. Thankfully, we can use python to script the process and compute t-stats and p-values at the same time:
#bigquerystandarderrors.py
#Nathaniel Lovin
#Technology Policy Institute
#
#!/usr/bin/env python
from google.cloud import bigquery
import math
import sys
from scipy.stats import t
client = bigquery.Client()
def rmse(model):
query = ("SELECT sqrt(mean_squared_error) as root_mean_squared_error "
"FROM ml.EVALUATE(MODEL `" + dataset + "." + model + "`)")
query_job = client.query(query)
result = query_job.result()
for row in result:
return row.root_mean_squared_error
def standef(model):
query = ("SELECT input, stddev FROM "
"ml.feature_info(MODEL `" + dataset + "." + model + "`)")
query_job = client.query(query)
result = query_job.result()
coeffs = {}
for row in result:
coeffs[row.input] = {'stddev': row.stddev}
return coeffs
def rsquared(data, coeffs):
for coeff in coeffs.keys():
query = ("CREATE OR REPLACE MODEL `" + dataset + "." + coeff + "` "
"OPTIONS (model_type='linear_reg', input_label_cols=['" + coeff + "']) AS "
"SELECT " + ", ".join(coeffs.keys()) + " FROM `" + dataset + "." + data + "` WHERE " + " is not NULL and ".join(coeffs.keys()) + " is not NULL")
query_job = client.query(query)
result = query_job.result()
query = ("SELECT r2_score FROM ml.EVALUATE(MODEL `" + dataset + "." + coeff + "`)")
query_job = client.query(query)
result = query_job.result()
for row in result:
coeffs[coeff]['r2_score'] = row.r2_score
return coeffs
def standarderror(root_mean, sqrtn, coeffs):
for coeff in coeffs.keys():
corr = math.sqrt(1-coeffs[coeff]['r2_score'])
error = root_mean/(sqrtn*coeffs[coeff]['stddev']*corr)
coeffs[coeff]['standard error'] = error
def coefficients(coeffs, dataset, model_name):
query = ("SELECT input, weight FROM (ML.FEATURE_INFO(MODEL `" + dataset + "." + model_name + "`) LEFT JOIN ML.WEIGHTS(MODEL `" + dataset + "." + model_name + "`) ON input = processed_input)")
query_job = client.query(query)
result = query_job.result()
for row in result:
coeffs[row.input]['coefficient'] = row.weight
dataset = sys.argv[1]
data = sys.argv[2]
model_name = sys.argv[3]
n = int(sys.argv[4])
sqrtn = math.sqrt(n)
root_mean = rmse(model_name)
coeffs = standef(model_name)
coeffs = rsquared(data, coeffs)
standarderror(root_mean, sqrtn, coeffs)
#The t-stat for the null hypothesis Beta_hat = 0 is Beta_hat/se(Beta_hat)
coefficients(coeffs, dataset, model_name)
for coeff in coeffs.keys():
coeffs[coeff]['tstat'] = coeffs[coeff]['coefficient']/coeffs[coeff]['standard error']
coeffs[coeff]['pvalue'] = 1-t.sf(coeffs[coeff]['tstat'], n-len(coeffs.keys())-1)
for coeff in coeffs.keys():
print(coeff + " coefficient: " + str(coeffs[coeff]['coefficient']))
print(coeff + " standard error: " + str(coeffs[coeff]['standard error']))
print(coeff + " t-stat: " + str(coeffs[coeff]['tstat']))
print(coeff + " p-value: " + str(coeffs[coeff]['pvalue']))Before running this script, make sure you have followed the instructions to set up the credentials in your current terminal session. Then use python to run this script as so:
python bigquerystandarderrors.py <dataset> <data> <model_name> <n>where <dataset> is the bigquery dataset where your model and data are located, <data> is the bigquery table with your data, <model_name> is the name of the original bigquery ml model, and <n> is the size of the sample.
This gives us the baseline OLS standard errors estimate. Issues like heteroskedasticity and autocorrelation can make the estimates inconsistent, which is why my next post will focus on how to compute robust standard errors with BigQuery.


